Об оценке коэффициентов в уравнении линейной регрессии / экологические процессы

Об оценке коэффициентов в уравнении линейной регрессии, описывающем изменения уровня воды в русле горной реки Мзымта

On the estimation of coefficients in the linear regression equation, which describes the changes in water level in the mainstream of the mountain river Mzymta

Е.А. Семенчин, Н.Г. Титов

E.A. Semenchin, N.G. Titov

Кубанский государственный университет

Данная работа посвящена оценке (методами регрессионного анализа) коэффициентов в уравнении линейной регрессии (математической модели), описывающем изменения уровня воды в русле горной реки Мзымта. Построена математическая модель изменений уровня воды в данной реке. На основе статистического материала о характеристиках паводка, имевшем место в октябре 2003 года в районе гидрологического поста этой реки, полученная модель была подвергнута проверке на адекватность экспериментальными данными.

This work is devoted to the evaluation (regression analysis) of the coefficients in the linear regression equation (mathematical model) that describes the changes in water level in the mainstream rock Mzymta. To construct a mathematical model of changes in water level in the river. On the basis of statistical data on the characteristics of the flood, which had a one hundred–ME in October 2003 in the hydrological position of the river, halftained model was subjected to a check on the adequacy of the experimental data.

Многие реки Краснодарского края относятся к рекам горного типа. Реки такого типа обладают определенными гидрологическими особенностями, существенно отличающими их от рек равнинного и горно–равнинного типов. Поэтому методики, описывающие изменения уровня воды в руслах рек рав-нинного и горно–равнинного типов, не применимы (как показывают вычислительные эксперименты) для описания изменения уровня воды в руслах рек горного типа. В данной работе предложена методика измерения колебаний уровня воды в русле реки Мзымта, относящейся к рекам этого типа. Точный прогноз повышения уровня воды позволит руководству ГУ «Краснодарский краевой центр по гидрометеорологии и мониторингу окружающей среды» (ГУ КЦГМС) заблаговременно предупреждать гражданское население о возможности возникновения паводковой ситуации на отдельных участках русла указанной реки. Цель работы – методами регрессионного анализа разработать методику прогноза изменений уровня воды в русле одной из рек горного типа – реке Мзымта (Краснодарский край). Для достижения поставленной цели были использованы статистиче-ские данные о метеоусловиях и уровне воды за июнь–август 2010 года, пре-доставленные ГУ КЦГМС.

Пусть значения уровня воды в реке Мзымта на момент времени $t_{i}$ совпадают со значениями функции $y(t_{i})=f(x_{1}(t_{i-3}),x_{1}(t_{i-2}),x_{1}(t_{i-1}),x_{2}(t_{i})),t_{i-3}<t_{i-2}<t_{i-1}<t_{i},i=3,4,...,n,$ (1)

где $y(t_{i})$ - прогнозируемый уровень воды в створе данной реки Мзымта в районе гидрологического поста, $x_{1}(t_{i-3}),x_{1}(t_{i-2}),x_{1}(t_{i-1})$ - уровень воды в моменты $t_{i-3},t_{i-2},t_{i-1}$ соответственно, $x_{2}(t_{i})$ – количество осадков, выпавших на момент $t_{i}$ в окрестности русла.

Пусть функция (1) является линейной:$y(t_{i})=b_{1}+a_{1}x_{1}(t_{i-3})+a_{2}x_{1}(t_{i-2})+a_{3}x_{1}(t_{i-1})+a_{4}x_{2}(t_{i})$ (2) где, $a_{1},a_{2},a_{3},a_{4}$ – некоторые постоянные.

На основе статистических данных методами регрессионного анализа были вычислены значения коэффициентов и свободного члена в (2) (см. табл.1).

Таблица 1. Значения коэффициентов и свободного члена в регрессионной модели (2)

b	–3,990373807
$a_{1}$	0,958433081
$a_{2}$	0,683938674
$a_{3}$	–0,628201975
$a_{4}$	–0,001390261

Согласно данным, приведенным в таблице 1, функция (2) (регрессионная модель) имеет вид: $y(t_{i})=-3,990374+0,95843x_{1}(t_{i-3})+0,683939x_{1}(t_{i-2})-0,628201x_{1}(t_{i-1})-0,00139x_{2}(t_{i})$ (3)

Точность оценки прогноза значений $y(t_{i})$ определяется числовыми значения-ми характеристик регрессионной модели (3), приведенными в таблице 2,

Таблица 2. Характеристики регрессионной модели (2)

$R^{2}$	0,993972
Нормированное значение $R^{2}$	0,993692
Стандартная ошибка σ	1,627712
Количество наблюдений n	91
F – критерий Фишера	3545,484

коэффициента детерминации

$R^{2}=1-{\frac {\sum _{i=1}^{n}(y_{i}-{\tilde {y}}_{i})^{2}}{\sum _{i=1}^{n}(y_{i}-{\bar {y}}_{i})^{2}}}$,(4)

и значением

$F+{\frac {R^{2}}{1-R^{2}}}\cdot {\frac {n-k}{k-1}}$,(5)

где n – размер выборки (количество проведенных замеров), k – число коэффициентов модели (3),$y_{i}$ – наблюдаемое значение y(t),${\tilde {y}}_{i}$ – значение y(t) вычисленное с помощью уравнения регрессии (3) в момент $t_{i}$, i=3, …, n, ${\bar {y}}_{i}$ – среднее значение y(t), вычисленное на основе статистических данных. Если F превышает некоторое критическое значение $F_{cr}$, определяемое по таблице значений F–критерия Фишера при заданных n, k и заданной доверительной вероятности $\alpha$, а величина $R^{2}$ близка к 1, то значение $y(t_{i})$, вычисленное по формуле (3), с вероятностью, близкой к 1, совпадает с экспериментальными данными. Согласно статистическим данным и допущениям, указанным выше, $F_{cr}=1,4170883451$, $\alpha =0,95,n=91,k=4,R^{2}=0,996982,F=3545,48$. Т.к. $F>F_{cr}(3545,48>1,4170883451)$, т.е. F во много раз превышает $F_{cr}$, то с вероятностью 0,95 при стандартной ошибке σ= 1,627712 значения $y(t_{i})$ совпадают с реальными значениями $y(t_{i})$, i=3, 4, …, n.

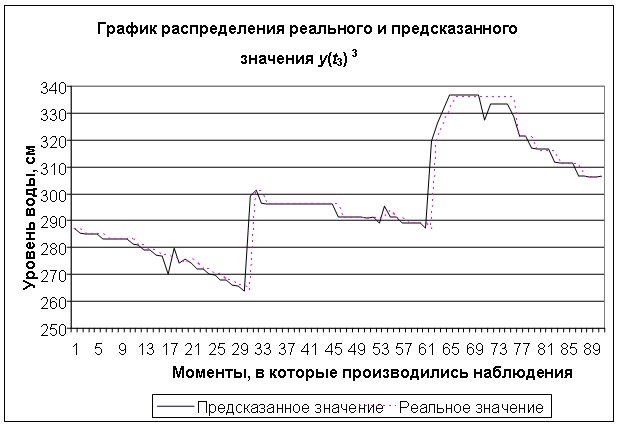
На рисунке 1 приведены графики значений y(t), построенные на основе статистических данных и значений регрессионной модели (3). Из этих гра-фиков видно, что прогнозируемые с помощью (3) значения $y(t_{i})$ несущественно отличаются от статистических данных.

Рис 1 – Графики значений y(t), построенные на основе статистических данных регрессионной модели (3)

---