Прогнозирование уровня воды в реке Мзымта на основе нейронной сети /экологические процессы

Прогнозирование уровня воды в реке Мзымта на основе нейронной сети имеющей архитектуру многослойного персептрона

Prediction of water level in the river Mzimta based neural network architecture having a multilayer perceptron

Е.А. Семенчин, Н.Г. Титов

E.A. Semenchin, N.G. Titov

Кубанский государственный университет

Данная работа посвящена описанию предлагаемой авторами статьи методики прогноза уровня воды в реке Мзымта (Краснодарский край), которая основана на использовании нейронной сети с архитектурой многослойного персептрона.

This work is devoted to a description of the proposed by the authors of Me-procedure was forecast water levels in the river Mzymta (Krasnodar region), which is based on neural network architecture with multi-layered perceptron.

На территории Краснодарского края находится много рек, которые следует отнести к рекам горного типа. В основном эти реки протекают в горных районах Сочи - Туапсе. Рекам такого типа свойственны высокая скорость течения и резкое изменение уровня воды в русле за счет обильных осадков, ледникового и снегового питания, что не так характерно для рек равнинного и горно-равнинного типов. Как показывают вычислительные эксперименты, методики, описывающие изменения уровня воды в руслах рек равнинного и горно-равнинного типов, не применимы для описания изменения уровня воды в руслах рек горного типа. Цель работы – разработать нейронную сеть с архитектурой многослойного персептрона для прогноза уровня воды в руслах горных рек, обучить ее с помощью метода обратного распространения, основной идеей которого является распространение сигналов ошибки от выходов сети к её входам, в на-правлении, обратном прямому распространению сигналов в обычном режиме работы.

Для достижения поставленной цели были использованы статистические данные о метеоусловиях на гидрологическом посту, расположенном на реке Мзымта, уровне воды в реке за июнь - август 2010 года, предоставленные Краснодарским центром гидрометеорологии и мониторинга окружаю-щей среды, пакет прикладных программ STATISTICA 6.1.

Предположим, что значения уровня воды в реке Мзымта в момент времени ti совпадают со значением функции $y(t_{i})=f(x_{1}(t_{i-3}),x_{1}(t_{i-2}),x_{1}(t_{i-1}),x_{2}(t_{i})),t_{i-3}>t_{i-2}>t_{i-1}>t_{i},t_{i}\epsilon [o,t],i=3,4,...,n,$ (1)

где $y(t_{i})$ – прогнозируемый уровень воды в створе данной реки в районе гидрологического поста, $x_{1}(t_{i-3}),x_{1}(t_{i-2}),x-1(t_{i-1})$ - уровень воды в моменты $t_{i-3},t_{i-2},t_{i-1}$ соответственно, $x_{2}(t_{i})$ - количество осадков, выпавших на момент $t_{i}$ в окрестности русла.

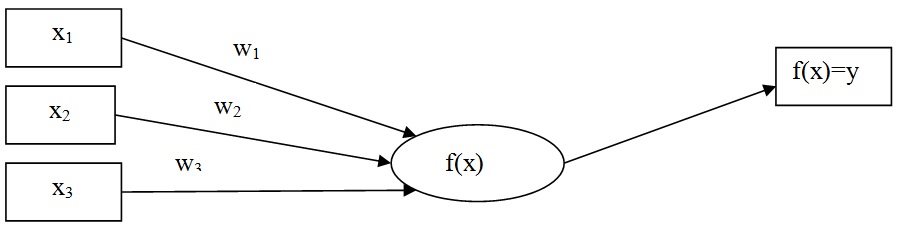
Архитектура построенной нейронной сети для прогноза паводков в русле указанной реки определяется как многослойный персептрон. Данная архитектура представлена в виде упрощенной схемы (см. рис. 1). В каждый нейрон подаются входные значения xi с некоторой поправкой в виде слагаемого $w_{i}$, затем эта сумма пропускается через передаточную функцию $f(x)$, значение которой подается на выход. Общая схема работы представлена на рис. 1, где $x_{1},x_{2},x_{3}$ –входные значения, поступающие в нейрон, тогда $w_{1},w_{2},w_{3}$ – синапсы трех входных дендритов соответственно, которые преобразуются передаточной функцией: $f(x)=f(w_{1}(x_{1})+w_{2}(x_{2})+w_{3}(x_{3})).$

Рисунок 1 – Общая схема работы

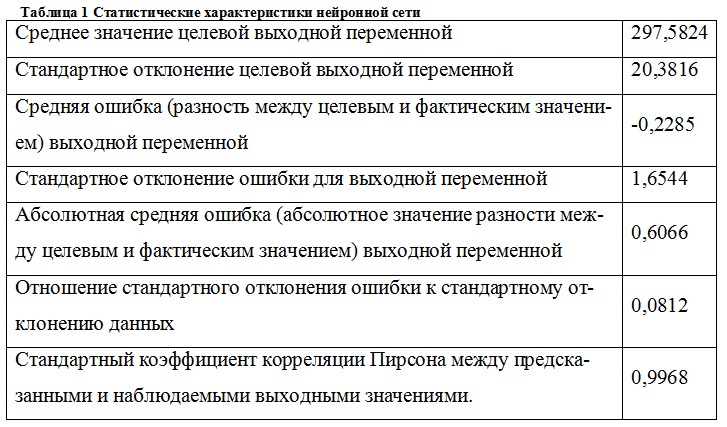
Для обучения данной нейронной сети были использованы данные об уровне воды и количества осадков в реке Мзымта за июнь-август 2010 года. Статистические характеристики построенной нейронной сети приведены в таблице 1.

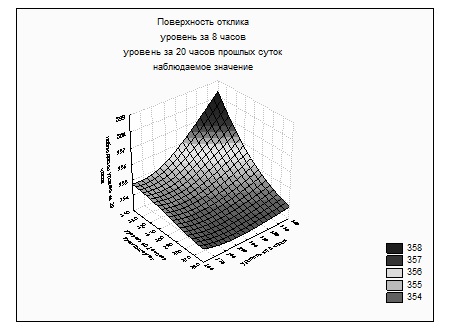
Как видно из таблицы 1 отношение стандартного отклонения ошибки к стандартному отклонению данных меньше 0,1, что указывает на достаточно высокую точность прогноза [1]. Отношение стандартных отклонений на обучающем подмножестве (производительность обучения данной сети) равно 0,0624355221762253, ошибка обучения, т.е. ошибка сети, полученная для обучающего подмножества, составила 0,0179139252837398. Построим гистограмму частоты остатков для нашей модели. Предположение о хорошей корреляции данных подтверждаются коэффициентом корреляции Пирсона, который близок к единице. Также имеет смысл рассмотреть поверхность отклика (см. рисунок 2), которая показывает влияние изменения двух входных (независимых) переменных на прогноз выходной переменной.

Рисунок 2 - Поверхность отклика. Влияние двух независимых переменных на прогнозируемую переменную

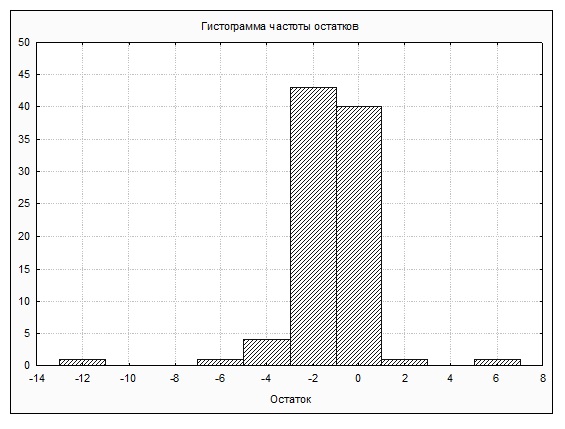
Для анализа остатков рассмотрим гистограмму частоты остатков представленную на рисунке 3.

Рисунок 3 - Гистограмма чистоты остатков

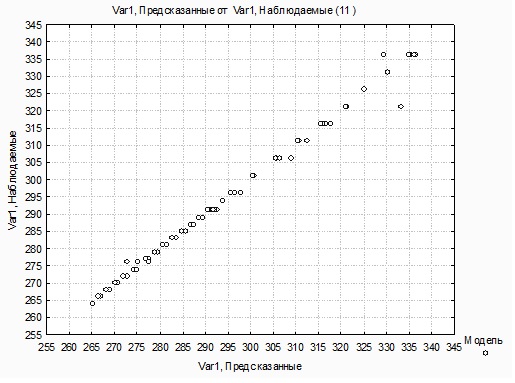
Как видно из рисунка 3 гистограммы частоты остатков вертикально симметрична, что подтверждает гипотезу о нормальном распределении остатков [2]. Рассмотрим диаграмму рассеяния предсказанных значений представленную на рисунке 4.

Рисунок 4 - Диаграмма рассеяния предсказанных значений

Как видно на рисунке 4, точки данной диаграммы располагаются на незначительном расстоянии от прямой $y=x$. Полученный результат указывает на адекватность модели экспериментальным данным [3].

Список литературы

1. Статистическое моделирование и прогнозирование под. ред. Гранборга. Москва: Финансы и статистика, 2000, – 383 с.
2. Ивченко, Г.И., Медведев, Ю.И. Математическая статистика: учеб. пособие для втузов. М.: Высш. шк.. 1984. – 248 с.
3. Крамер Г. Математические методы статистики. М.: Мир. 1975. ─375 с.
4. Рябушкин Т.В. Общая теория статистики: учебник / Т.В. Рябушкин, М.Р. Ефимова, Н.И. Яковлева. М.: Финансы и статистика. 1981. – 346с.
5. Гусаров В.М. Теория статистики, М.: ЮНИТИ. 2001. – 247 с.
6. Тюрин Ю.Н. Теория вероятностей и статистика / Тюрин Ю.Н., Макаров А.А., Высоцкий И.Р., Ященко И.В. М.: МЦНМО. 2008. – 256с.

---